写像の話

ちょっと勉強したい大人のための数学教室

写像の話

1. 写像とは・・・

写像とは、ある集合の要素と、他の集合の要素を対応付ける仕組みのことです。
写像を f とした場合、要素 x に対し、 f によって対応付けた要素を f(x) と表記します。

たとえば、以下のように実数の集合同士を対応付けるとします。

∀x ∈ R ⇒ f(x) = x ∈ R

この写像は、高校数学で y = x と記述する関数と同義です。

写像と関数の違いは明確ではありませんが、慣習的に f(x) が実数や複素数になるものを関数、それ以外を写像と言っています。

ある集合 V に対し、 { f(x) ; ∀ x ∈ V } となる集合を f の像と言います。

2. 単射とは・・・

単射とは、ある集合の要素を一つ決定したとき、対応付けられた他の集合の要素が一意に決定する写像の事を言います。
すなわち、f : A →B が単射である場合、集合A の要素 a に対応する f(a) は、集合 B の中に一つしか存在しないことになります。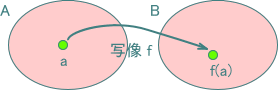

写像 f が単射であるということを数学的に記述すると以下のようになります。

∀a ∈ A, ∃1 b∈B s.t. f(a) = b

たとえば、{日本人の集合} と {都道府県} を関連付ける写像 f を出身地とした場合、この写像は単射になります。実際に、