HOME > Mathematical World > 集合の基礎２

ちょっと勉強したい大人のための数学教室

集合の基礎2

1. 差集合とは・・・
差集合とは、「ある集合から、指定された他の集合を除いた要素の集合」のことです。
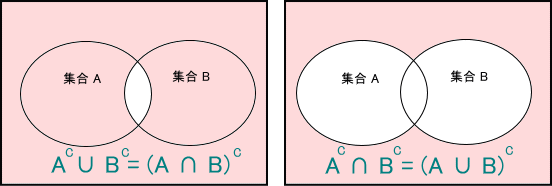
たとえば、「数学者」の集合から、「男」の集合を除くと、「女性数学者」の集合になりますが、これは、「数学者」の集合から「男」の集合を除いた差集合ということになります。
差集合＝ある集合から、指定された他の集合を除いた要素の集合
A1 = {a1,a2,a3,a4,a5} から A2 = {a1,a7} を除いた差集合は、{a2, a3, a4, a5} になります。

差集合は \ という記号を使用します。
集合 A と集合 B の差集合は、A \ B と記述します。

べん図を使用して、差集合を表現すると、下図のようになります。（色付きの箇所）

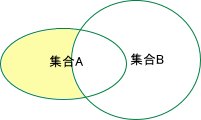
（例 1-1）
カミセンの集合 = V6 の集合 \ トニセンの集合

（例 1-2）
有利数の集合 = 実数の集合 \ 無理数の集合


2. 補集合とは・・・
補集合とは、ある集合に含まれていない要素の集合のことです。
わかりやすく表現すると、「ある集合以外」ということになります。
補集合を考える際には、全体集合という境界線が必要になります。

たとえば、全体集合をビートルズの集合とし、ギタリストの集合の補集合は、{ポール・マッカートニー（ベーシスト）, リンゴ・スター（ドラマー）} になります。

補集合＝ある集合に含まれていない要素の集合

また、全体集合を X1 = {a1, a2, a3, a4, a5} としたとき、A = {a1, a2} の補集合は {a3, a4, a5} になります。
一方、全体集合を X2 = {a1, a2, a3, a4, a5, ・・・,a10} としたとき、A = {a1, a2} の補集合は {a3, a4, a5,・・・a10} になります。

つまり、同じ集合の補集合であっても、全体集合をどう定義するかによって、属する要素が違ってきます。

補集合は、C という記号を使用します。
集合 A の補集合は AC と記述します。
（例 2-1）（全体集合を自動車）
国産車の集合 = 外車の補集合

（例 2-2）（全体集合を実数）
有理数の集合 = 無理数の補集合


3. ド・モルガンの法則とは・・・
集合論で有名な法則の一つにド・モルガンの法則があります。
[定理 3-1]（ド・モルガンの法則）

(1) AC ∪ BC = (A ∩ B)C
(2) AC ∩ BC = (A ∪ B)C
これはベン図を使用すると、イメージ的につかめやすくなります。


4. 有限・無限集合とは・・・
有限集合とは、集合を構成する要素が有限個の場合、その集合を有限集合と言います。
有限集合＝要素の数が有限個である集合
たとえば、学校の集合を {小学校、中学校、高校、専門学校、大学} とすると、これは、要素が5 つの有限集合ということになります。

一方、無限集合とは、集合を構成する要素が無限個の場合、その集合を無限集合と言います。
無限集合＝要素の数が無限個である集合
たとえば、自然数の集合は {1, 2, 3, ・・・ } と要素の数が無限にあるので、無限集合ということになります。