HOME > Mathematical World > 集合の基礎１

ちょっと勉強したい大人のための数学教室

集合の基礎1

1. 集合とは・・・
集合とは、「ある条件に当てはまる要素の集まり」のことです。
たとえば、「日本国籍を有している人間」という条件を満たす要素の集まりで、「日本人」という集合になります。
集合＝ある条件に当てはまる要素の集まり
集合は、{ } で囲んで表現することにします。
{ } の中は要素の全てを記述するか、集合の条件を記述します。
（例 1-1）
SMAPの集合 = { 中居正広, 木村拓哉, 稲垣吾郎, 草なぎ剛, 香取慎吾}

（例 1-2）
自然数の集合 = { 1 以上の整数 }
ある集合 X に対し、x が X の要素であるとき x ∈ X と記述します。
これを利用し、集合を以下のように記述することもあります。
（例 1-3）
自然数の集合 = { x ∈ 数の集合 ; x ≧ 1 でありかつ整数}
{ } 内の ; の左側に要素、右側に条件を記述します。


2. 和集合とは・・・
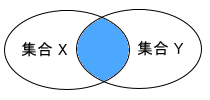
和集合とは、複数の集合の要素全体の集合のことです。
たとえば、V6 の集合は、トニセンの集合とカミセンの集合の和集合になります。
和集合＝複数の集合の要素全体の集合
A={a1,a2,a3} と B={b1,b2,b3,b4,b5} の和集合は {a1,a2,a3,b1,b2,b3,b4,b5} になります。

和集合は、∪という記号を使用します。
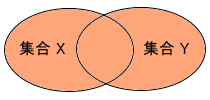
集合 A と集合 B の和集合は A ∪ B と記述し、集合A1,・・・,An までの和集合は A1 ∪ ・・・ ∪ An と記述します。
（例 2-1）
県民の集合 = 市民の集合 ∪　町民の集合 ∪ 村民の集合

（例 2-2）
整数の集合 = 正の数の集合 ∪ 負の数の集合 ∪ { 0 }
このとき以下のことが成立します。
[定理 2-1]
x ∈ X ∪ Y ならば x ∈ X または x ∈ Y である。
逆に x ∈ X または x ∈ Y ならば x ∈ X ∪ Y である。
(証明)
x ∈ X ∪ Y　と仮定します。
和集合の定義より、X ∪ Y は、X および Y の要素全体の集合です。
したがって、x は X もしくは Y いずれかの要素になっているはずです。

逆に x ∈ X と仮定します。
定義より X ∪ Y は、X および Y の要素全体の集合ですから、x ∈ X ∪ Y になります。
これは x ∈ Y も同様に成立します。
例 1-1 を例にすると、石川県民は、金沢市民か、もしくは他市町村民であり、逆に金沢市民は、石川県民であることになります。


3. 積集合とは・・・
積集合とは、複数の集合の要素の中で、すべての集合に属している要素全体の集合のことです。
たとえば、{高橋愛, 加護愛, 辻希美} の集合は、モーニング娘。の集合とミニモニの集合の積集合になります。
積集合＝すべての集合に属している要素全体の集合
A1={a1,a2,a3} と A2={a1,a2,a4,a5} の積集合は {a1,a2} になります。

積集合は、∩という記号を使用します。
集合 A と集合 B の積集合は A ∩ B と記述し、集合 A1,・・・An までの積集合は A1 ∩・・・∩An と記述します。
（例 3-1）
太鼓の集合 = 打楽器の集合 ∩ 和楽器の集合

（例 3-2）
正四角形の集合 = 四辺の長さが等しい図形の集合 ∩ 頂点が90度の図形の集合
このとき以下のことが成立します。
[定理 3-1]
x ∈ X ∩ Y ならば x ∈ X かつ x ∈ Y である。
逆に x ∈ X かつ x ∈ Y ならば x ∈ X ∩ Y である。
(証明)
x ∈ X ∩ Y　と仮定します。
積集合の定義より、X ∩ Y は、X および Y のいずれにも属している要素全体の集合です。
したがって、x は X および Y の要素になっているはずです。

逆に x ∈ X かつ x ∈ Y と仮定します。
定義より X ∩ Y は、X および Y のいずれにも属している要素全体の集合です。
したがって、x ∈ X ∩ Y になります。


4. 部分集合とは・・・
部分集合とは、ある集合の要素の一部（もしくは全体）を取り出した集合のことです。
たとえば、大学生の集合は、学生全体の集合の部分集合になります。
部分集合＝ある集合の要素の一部（もしくは全体）を取り出した集合
A1 = {a1, a2} は X = {a1, a2, ・・・,an} の部分集合になります。

A1 が X の部分集合である場合、A1 ⊂ X もしくは　X ⊃ A1 と記述します。
（例 4-1）
セリーグの球団の集合 ⊂ プロ野球の球団の集合

（例 4-2）
正の数の集合 ⊂ 数の集合

このとき、定理2-1、定理3-1より、以下のことが成立します。
[定理 4-1]
集合 X, Y に対し、
(1) X ⊂ X ∪ Y
(2) X ∩ Y ⊂ X
(証明)
(1)について
x ∈ X と仮定します。
定理 2-1 より、x ∈ X ∪ Y です。したがって X ⊂ X ∪ Y になります。

(2)について
x ∈ X ∩ Y と仮定します。
定理 3-1 より、x ∈ X です。したがって X ∩ Y ⊂ X になります。


5. 空集合とは・・・
空集合とは、要素がない集合のことです。
空集合＝要素がない集合
A1 = { } は空集合になります。

通常、空集合は Φ で記述します。

このとき、定理4-1より、以下のことが成立します。
（自明であるので、特に証明は行いません。）
[定理 5-1]
集合 X に対し、
(1) Φ = X ∩ Φ
(2) X = X ∪ Φ


6. べん図とは・・・
べん図とは、集合をイメージ化し、より捉えやすくした図のことです。
たとえば、集合 X のみをべん図で表現すると、以下のようになります。

べん図は、他の集合との関係を捉えたい場合に、効力を発揮します。
たとえば、大学出身者の集合と政治家の集合をべん図で表現してみると、以下のようになります。

重なった箇所が「政治家のうち、大学出身者」の集合です。
（例 6-1）
集合 X と集合 Y の和集合（塗りつぶし部分が和集合）

（例 6-2）
集合 X と集合 Y の積集合（塗りつぶし部分が積集合）

（例 6-3）
集合 X が集合 Y の部分集合